Durata
2 ore di lezione, ma suggeriamo di ripetere questo tipo di consegna più volte alla settimana, anche per brevi periodi, in modo da rafforzare questo modo di rappresentare i numeri.
Preparazione e Consegna
L'insegnante propone esercizi sulla rappresentazione dei numeri sull’abaco e sulla scomposizione in decine ed unità.
Materiale
Gli abaci personali;
FASE 1
1) Chiedere ai bambini di rappresentare i numeri della scheda allegata sul proprio abaco:
2) Consegnare ai bambini una scheda ciascuno.
Nei disegni dell’abaco che rappresenta i numeri, far scrivere sotto ciascuna fila di palline il numero di palline che rappresenta. Per esempio:
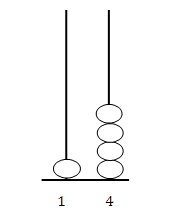 :
:
Promuovere una discussione collettiva con domande come:
“Come avete rappresentato i numeri più grandi del 9?"
"Come li avete pensati prima di fare il disegno?“
"Come si può leggere il numero scritto sotto il disegno dell’abaco?"
Scrivere
insieme sul quaderno le conclusioni.
FASE 2
Ogni bambino ha il suo abaco e l’insegnante chiede:
Prendi 3 unità,
aggiungi 2 unità …
ancora 2 unità …
aggiungi 1 decina
e ancora aggiungi 1 unità …
Riparti da 0:parti da 2 unità …
aggiungi 3 unità …
aggiungi 2 decine,
più altre 3 unità …
togli una decina
Riparti da 0:
6 unità ...
più 2 unità ...
più 3 unità ...
meno una decina
È bene usare tutti i sinonimi di addizionare: “aggiungi”, “metti ancora”, “più”, “prendi altre”…
Analogamente si possono proporre le stesse consegne facendo “togliere”, (“diminuire”, “meno”…) le unità e decine.
Che cosa aspettarsi
Nella prima fase dell'attività gli studenti potrebbero ancora avere
difficoltà con questo tipo di rappresentazione, perchè per loro ancora
"priva di senso". In
questo caso si deve usare una pallina (di quelle che sono
anche messe come unità) e magicamente “vale 10” se viene infilata
nella seconda asticella. Questo è davvero difficile perché richiede un
passo di astrazione: quello che prima con le cannucce era 1
fascetto-decina (ma vedevo e sentivo ancora il 10) ora è 1 pallina,
analoga a quelle delle unità (come le cannucce sciolte che però
avevano uno stato molto diverso a livello cinestetico rispetto al
fascetto-decina).
Nella seconda fase è possibile che gli
studenti trovino difficoltà ogni volta che si passa dal 9 al 10 e dal
10 al 9, perchè le azioni di "sfilare" e "infilare"
richiedono un aumento delle risorse cognitive rispetto a quelle
coinvolte per rispondere alle altre situazioni.
Significati matematici che si vogliono costruire
Si vuole aiutare l’apprendimento della notazione decimale e l’interpretazione dei, rafforzando i legami tra codice arabico, verbale e semantico. Composizione e scomposizione dei numeri a due cifre in decine ed unità.
Come costruire i significati matematici
Dalle discussioni collettive possono emergere diversi modi di pensare. Per esempio: “Penso di riempire l’asta di destra e quando arrivo a 10 metto una pallina sull’asta a sinistra e poi vado avanti a mettere palline a destra fino a che arrivo al numero da rappresentare; cerco di capire quante decine contiene il numero e le rappresento sull’asta di sinistra e poi metto tante palline quante sono le unità sull’asta di destra.”
Dalla seconda domanda per la discussione si vuole guidare la terminologia verso risposte come: “quattordici” oppure scomponendolo nelle “decine” e “unità”, quindi “1 decina e 4 unità”. È bene usare il termine “pallina-decina” per le palline della colonna di sinistra, se serve nella discussione per distinguere le palline-unità di destra da quelle della colonna di sinistra.
Possibili conclusioni da riportare sul quaderno sono:
Le singole palline sull’asta di destra vengono chiamate unità (u). Le palline sull’asta di sinistra vengono chiamate decine (da), proprio perché le palline su quest’asta valgono quanto 10 delle palline sull’asta di destra. In altre parole, una pallina-decina (da) vale 10 palline-unità (u).
Con l’abaco abbiamo scoperto che il nostro sistema è decimale sia perché per scrivere i numeri usiamo 10 cifre
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9) sia perché si fanno dei raggruppamenti da 10 per passare da una posizione all’altra. Questo deriva anche dal fatto che abbiamo 10 dita.
Inoltre il nostro sistema è posizionale: il valore di una cifra dipende dalla sua posizione nella scrittura del numero. Lo stesso simbolo in posizione diversa ha significato diverso (per esempio pensiamo allo 0).
Il nostro sistema numerico è decimale-posizionale.
.
| Contare intransitivo | |
| Contare transitivo | sì, è possibile |
| Aspetto ordinale del numero | |
| Aspetto cardinale del numero | sì |
| rappresentazioni del numero | simbolico e analogico |
| Confronto fra numeri | sì |
| Abbinamento quantità/numero | sì |
| Problemi additivi (addizione-sottrazione) | si |
| Spazio e figure | |
| Artefatti/strumenti | Abaco |
Schede e possibili compiti
Proporre schede come quelle presenti nei Materiali allegati.
Alcuni esercizi suggeriti, a supporto dell’attività, con l’uso di programmi software.