PERCORSI E
LABIRINTI
Durata: Due-tre ore.
Preparazione e Consegna
FASE 1
Mostrare i seguenti due percorsi (alla lavagna, con proiettore, o su carta)
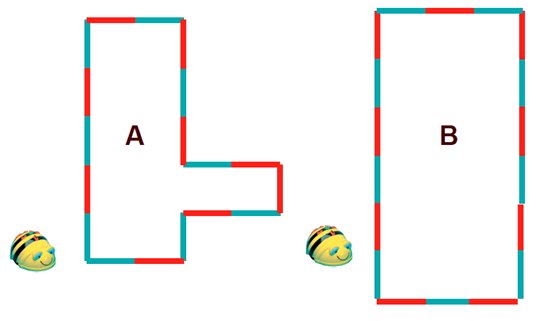
porre le seguenti domande:
a) Se il bee-bot a sinistra fa il percorso A e quello di destra il percorso B, quale bee-bot ci mette più tempo a finire? Perché?
b) Quale bee-bot avrà fatto il viaggio più lungo? Perché?
c) Controlla le tue risposte programmando bee-bot perché faccia i due percorsi.
FASE 2
Coprite alcune righe e colonne della griglia costruita (10x10) in modo da ottenere una griglia 7x5 come questa. Oscurate (o segnate) le caselle corrispondenti a quelle nere e posizionate l’immagine di una casa nell’angolo corrispondente.
Aiuta bee-bot a tornare a casa. Programmalo perché faccia il percorso più breve e non passi sulle caselle nere.
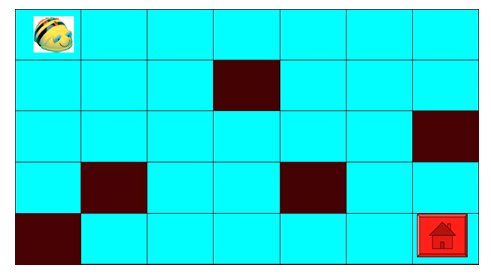
FASE 3
Come sopra, create sulla griglia costruita la seguente immagine:
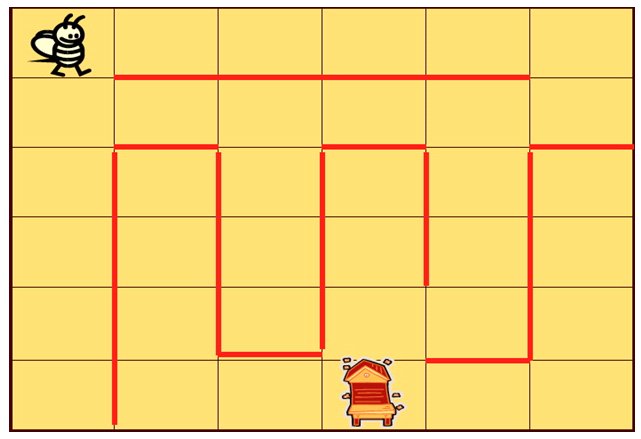
Aiuta bee-bot a tornare al suo alveare. Programmalo perché faccia il percorso più breve e non passi sulle linee rosse.
Che cosa aspettarsi
La situazione è volutamente problematica: “più tempo” impiegato e viaggio “più lungo” non vogliono necessariamente dire la stessa cosa e dovrebbero emergere riflessioni implicite dei bambini sui termini ambigui.
Significati matematici che si vogliono costruire
Questa attività vuole continuare ad esplorare la nozione di “lunghezza” di un percorso ed arrivare a cenni della topologia della griglia, misurando percorsi in passi del bee-bot oppure in numero (minimo) di comandi necessari perché esegua un determinato percorso. Infine con questa attività si propone un lavoro a livello meta-cognitivo di riflessione su passi utili per la programmazione in questo contesto. Inoltre, dovendo pianificare, programmare, e verificare le sequenze programmate, l’attività dovrebbe aiutare a sviluppare abilità di pianificazione, visualizzazione, e uso di un linguaggio comune simbolico.
| Contare intransitivo |
|
| Contare transitivo |
sì, è possibile |
| Aspetto ordinale del
numero |
|
| Aspetto cardinale del
numero |
|
| Rappresentazioni del
numero |
|
| Confronto fra numeri |
|
| Abbinamento quantità/numero |
si |
| Problemi additivi
(addizione-sottrazione) |
|
| Spazio e figure |
si |
| Artefatti/strumenti |
Bee.bot |
Come cominciare a costruire significati matematici
Impostare una discussione intorno alle produzioni dei bambini rispetto alla prima consegna. Si può aiutare loro ad esplicitare i significati che danno a percorso che “dura di più nel tempo” e a percorso “più lungo”. Come per l’attività precedente, il percorso può essere visto e “misurato” in almeno due modi: contando il numero di comandi dati a bee-bot (in particolare questo influenzerà la durata temporale del percorso in modo che percorsi con lo stesso numero di comandi avranno la stessa durata temporale), oppure contando il numero di passi (traslazioni) di bee-bot (in questo caso il percorso più breve per arrivare da un punto A ad un punto B sarà quello che prevede il minimo numero di traslazioni orizzontali e verticali, ovvero la lunghezza della “L” che si forma percorrendo la griglia da A all’altezza di B e poi girando di 90 gradi per arrivare a B lungo la seconda direzione).
Possibili Compiti
A seconda di quello che emerge in classe proporre esercizi simili a cui pensare a casa e poi controllare le programmazioni in classe.
documento
PDF
Inizio pagina
|


